祭系に対してはβ＝Ω（昇交点経度）になるし、また地球固定座標系ではβ＝Ω（昇交点経度）−Ac（グリニジ時角、衛星が近地点通過時間tpにおける経度0度と春分点の間の角度）−ωe（地球の自転速度）×（t（現在の時間）−tp）となる。この座標変換を行うと

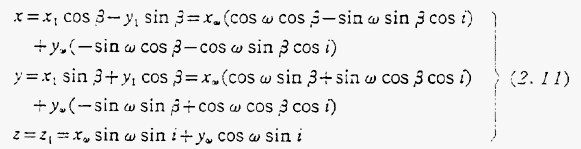
衛星の刻々の位置を直交座標系で求めることができる。

いままでの議論は人工衛星と地球という2つの物体の相互作用の形で考えてきた。この場合、衛星は地球に対して同じ軌道を回り続けるが、宇宙には地球のほかに月や太陽などの天体があり、それらの引力が人工衛星の運動にわずかではあるが影響を与えることになる。また、地球のかなり上方までわずかではあるが空気が存在（電離層はこのような気庫がイオンと電子に電離して生ずる）しており、その空気抵抗によって衛星の速度がわずかずつではあるが遅くなる効果もある。

また、後でも述べるとおり、地球は赤道方向に若干のふくらみをもった回転楕円体であり、前述のケプラの法則では、地球の中心に重力が集中したいわゆる均一の球体として考えられていたのとは違って地球のまわりての重力場に不均一さがあるので、これが人工衛星の運動に利の影響が生ずることになる。

このような原因で人工衛星の軌道要素はゲプラの法則によるものからわずかずつ変化していくことになる。

静止衛星

前述したようにケプラーの第3法則では、軌道の長半径Aと周期丁の問に、A3/T2＝一定の関係があり、遠心力と重力の加速度が釣合う（等しい）という関係から、円軌道では、衛星の軌道上の速度Vは

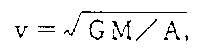
6,607×10−3?/g−S2,Mは地球の質量M＝5,975×10日gである。ここでAは軌道半径であるから、A＝R＋H,Rは地球の半径、R＝6,370?、Hを地球上の高さとすると：

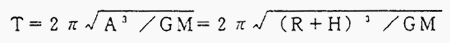
この式から地上からの高さ約36000?の円軌道に上げた衛星は24時間の周期を持つことが分かる。このような衛星が、地球の赤道上を東向き（地球の回転と同一方向）に回ると、地球の自転と衛星の軌道上の動きは完全に同期をするので、地上の各点から衛星は赤道上に止まったように見える。これが静止衛星である。

静止衛星を打上げるのには、まず、衛星をその軌道の地球から最も遠い点（遠地点）が、静止衛星の高度の近くになるような長楕円軌道（これを遷移軌道という）に上げ、遠地点で、衛星に付属している遠地点モータと呼ばれる推進器を吹かせて、赤道を回る円軌道（ドリフト軌道）に入れる。ついで、衛星付属の推進

前ページ　　　目次へ　　　次ページ